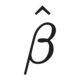This article is part of an extended series of tutorials for time-to-event (or survival) analysis. The next article is here.
Introduction
The four previous articles that I wrote were based on non-parametric methods in survival analysis. This is mainly because the book1 I referred to was based on applications in medicine, where the aim of the analysis is mostly (although not exclusively) inference rather than prediction, and non-parametric and semi-parametric methods lend themselves well to such applications. Since my main interest lies in applications in reliability, the ability to make predictions is important and parametric methods are useful in such cases.
The following article demonstrates the application of parametric regression modeling to data from a life test of ceramic ball bearings and is from a paper by McCool (1980)2. The methods that I employ in this analysis are from another excellent book3 that I have been referring to recently and came across the ceramic data set in the same book. The data set is also publicly available on DataShare, Iowa State University’s open data repository which can be accessed through this link.
The R statistical programming language is used for all computations and plots below. Unlike my previous articles, I have not included any R code within the article, but they are available on my Github page and can be accessed here. The code for some of the plots are lengthy and I wanted to avoid code chunks taking up space on this page.
Exploratory Analysis
Ten specimens were tested at each of the four levels of stress, as shown in table 1 below. The time-to-failure is recorded in terms of “Millions of Revolutions”.
| Millions of Revolutions | Stress (Mpsi) |
|---|---|
| 1.670 | 0.87 |
| 2.200 | 0.87 |
| 2.510 | 0.87 |
| 3.000 | 0.87 |
| 3.900 | 0.87 |
| 4.700 | 0.87 |
| 7.530 | 0.87 |
| 14.700 | 0.87 |
| 27.800 | 0.87 |
| 37.400 | 0.87 |
| 0.800 | 0.99 |
| 1.000 | 0.99 |
| 1.370 | 0.99 |
| 2.250 | 0.99 |
| 2.950 | 0.99 |
| 3.700 | 0.99 |
| 6.070 | 0.99 |
| 6.650 | 0.99 |
| 7.050 | 0.99 |
| 7.370 | 0.99 |
| 0.012 | 1.09 |
| 0.180 | 1.09 |
| 0.200 | 1.09 |
| 0.240 | 1.09 |
| 0.260 | 1.09 |
| 0.320 | 1.09 |
| 0.320 | 1.09 |
| 0.420 | 1.09 |
| 0.440 | 1.09 |
| 0.880 | 1.09 |
| 0.073 | 1.18 |
| 0.098 | 1.18 |
| 0.117 | 1.18 |
| 0.135 | 1.18 |
| 0.175 | 1.18 |
| 0.262 | 1.18 |
| 0.270 | 1.18 |
| 0.350 | 1.18 |
| 0.386 | 1.18 |
| 0.456 | 1.18 |
The plot of revolutions vs stress on linear axes and on log-log axes are shown in Fig.1 and Fig.2 below. The plot on the log-log axes suggests a linear relationship between log revolutions and log stress. Hence, we will consider the log transformation later in the article in the regression model.
Figure 1: Plot of Millions of Revolutions vs Stress (Mpsi) on linear axes.
Figure 2: Plot of Millions of Revolutions vs Stress (Mpsi) on log-log axes.
Notice the outlier data point at stress 1.09 Mpsi in Fig.2. When we notice such outliers, it is worth digging deeper into the test that resulted in this value and making sure that this is indeed a valid data point.
Probability Plots
The log location scale distribution model is shown in Eq. A below.
\[ \hspace{-2cm} \begin{align*} F(t;\mu,\sigma) & = Pr(T\le t)\\ & = \Phi \left[\frac{log(t)-\mu}{\sigma}\right] \tag{Eq. A} \end{align*} \] The distribution of \(\Phi\) determines the time-to-failure distribution. For example, if \(t\) is assumed to have a Weibull distribution, \(\Phi\) is the cumulative distribution function (CDF) of the standard smallest extreme value (SEV) distribution. Similarly, if \(t\) is assumed to have a log-normal distribution, then \(\Phi\) is the CDF of the standard normal distribution.
The log-normal and Weibull distributions are widely used in describing time-to-failure distributions in reliability applications. Weibull distribution offers flexibility by allowing the modeling of different shapes of the failure rate (increasing, decreasing or constant) while log-normal distribution has shown to be a good distribution to describe those failures that are of a fatigue-stress nature.
Probability plots for each level of stress are plotted on two different graphs below. Fig.4 shows a log-normal probability plot and Fig.5 shows a Weibull probability plot.
Figure 3: Log-normal plot
Figure 4: Weibull plot
The points on the plot are the non-parametric CDF estimates4 and the lines are based on the ML (maximum likelihood) estimates of the respective distribution parameters.
Looking at both plots in Fig.4 and Fig.5, there is nothing to suggest that either plot deviates too much from the assumed distributions. In fact, in many applications, several parametric models may provide reasonable fits to the data5. We are mainly looking for any indication that a particular distribution is definitely not a good fit, rather than proving that the data fits a particular distribution. The paper by McCool(1980) uses a Weibull distribution to model this data. We will continue with the same distribution and revisit this assumption later.
Notice that the outlier observation at 1.09 Mpsi stress can again be seen in the lower left corner of the log-normal and Weibull probability plots in Fig.3 and Fig.4.
Table 2 shows the ML estimates of the parameters \(\mu\) and \(\sigma\) when time-to-failure is assumed to be distributed Weibull. These are the paramters used to plot the ML fit lines in Fig.4.
| \(\hat{\mu}\) | \(\mathrm SE_{\hat{\mu}}\) | \(\hat{\sigma}\) | \(\mathrm SE_{\hat{\sigma}}\) | |
|---|---|---|---|---|
| 0.87 Mpsi | 2.330 | 0.353 | 1.050 | 0.248 |
| 0.99 Mpsi | 1.475 | 0.212 | 0.635 | 0.166 |
| 1.09 Mpsi | -1.030 | 0.230 | 0.696 | 0.173 |
| 1.18 Mpsi | -1.335 | 0.170 | 0.509 | 0.129 |
The log likelihood of the separate distributions is -46.602 with 8 parameters.
Plotting all the stress levels on the same plot helps in assessing the commonly used assumption that the Weibull shape parameter \(\sigma\) is constant across all stress levels. The slope of the ML fit line is related to the shape parameter \(\sigma\). The slopes of the lines in Fig.4 do look approximately similar for the stress levels 0.99 Mpsi, 1.09 Mpsi and 1.18 Mpsi, but is slightly different for the stress level 0.87 Mpsi. This is also evident in Table 2, where the \(\hat{\sigma}\) for 0.87 Mpsi stress is different as compared to the \(\hat{\sigma}\) at other levels of stress. But are these differences practically significant? I think it is difficult to answer this question, especially if one doesn’t have a lot of experience analyzing fatigue-stress data. Nevertheless, we will try to answer this question through a likelihood ratio (LR) test now and revisit this assumption later. The LR test compares the model with separate distributions consisting of 8 parameters (4 \(\mu\) and 4 \(\sigma\)) and the model where the shape parameter is constrained to be equal across all levels of stress, consisting of 5 parameters (4 \(\mu\) and 1 \(\sigma\)).
Figure 5: Weibull plot with the shape parameter constrained to be equal across all stress levels
Fig.5 above shows a Weibull plot where the shape parameter is constrained to be equal across all levels of stress, which is why the slopes of the lines are exactly the same.
Even with the applied constraint, the ML lines in Fig.6 look like a fairly decent fit to the non-parametric CDF estimates for all stress levels except the 0.87 Mpsi stress level. Table 3 shows the maximum likelihood estimates of the ML lines in the constrained model.
| \(\hat{\mu}\) | \(\mathrm SE_{\hat{\mu}}\) | \(\hat{\sigma}\) | \(\mathrm SE_{\hat{\sigma}}\) | |
|---|---|---|---|---|
| 0.87 Mpsi | 2.521 | 0.247 | 0.745 | 0.251 |
| 0.99 Mpsi | 1.435 | 0.238 | 0.745 | 0.251 |
| 1.09 Mpsi | -1.048 | 0.238 | 0.745 | 0.251 |
| 1.18 Mpsi | -1.411 | 0.237 | 0.745 | 0.251 |
The log likelihood of the constrained model is -49.015 with 5 parameters.
Conducting a likelihood ratio test will help determine whether the model with separate distributions for each level of stress, which contains 8 parameters (4 \(\mu\) and 4 \(\sigma\)) is statistically different to the model with the shape parameter constrained, which contains only 5 parameters(4 \(\mu\) and 1 \(\sigma\)).
\[ \begin{align*} \hspace{-2cm} \chi^{2}_{LR} & = 2(LL_{separate} – LL_{constrained})\\ & = 2(-46.6 – (-49.01)) = 4.82 \end{align*} \] The p-value for the LR test with the \(\chi^{2}_{LR}\) statistic as shown above and 3 degrees of freedom (8 parameters – 5 parameters) is 0.185. There is no evidence that both models are different at the 5% significance level. We will proceed with the assumption that the \(\sigma\) is the same at all levels of stress for now and revisit later, if required.
Weibull Regression
The Weibull regression model we consider is of the form:
\[ \hspace{-4cm} \begin{align*} F(t;\beta_{0},\beta_{1},\sigma) & = Pr(T\le t)\\ & = \Phi\left[\frac{log(t)-(\beta_{0}+\beta_{1}log(stress))}{\sigma}\right] \tag{Eq. B} \end{align*} \] where \(\sigma\) is constant across all stress levels and \(\Phi\) is the standard smallest extreme value distribution. It makes sense to take the log transformation of the stress variable since Fig.2 shows a somewhat linear relationship between logarithm of revolutions and logarithm of stress.
Table 4 shows the ML estimates, standard errors and the Wald 95% confidence intervals of \(\beta_{0}\), \(\beta_{1}\) and \(\sigma\) from the model in Eq.B.
| ML estimate | Standard Error | Wald Lower 95% CI | Wald Upper 95% CI | |
|---|---|---|---|---|
| \(\hat{\beta_{0}}\) | 0.789 | 0.148 | 0.498 | 1.079 |
| \(\hat{\beta_{1}}\) | -13.890 | 1.290 | -16.419 | -11.361 |
| \(\hat{\sigma}\) | 0.858 | 0.106 | 0.673 | 1.094 |
The log likelihood of this model is -54.402.
Fig.6 shows a Weibull plot of the regression model.
Figure 6: Weibull plot of the regression model
Clearly, a lack of fit is observed in Fig.6, where the ML fit lines do not seem to align very well with the non-parametric estimates denoted by the points, especially at the lower stress levels. Conducting a likelihood ratio (LR) test between the 5 parameter constrained \(\sigma\) model and the 3 parameter regression model, we get:
\[ \begin{align*} \hspace{-2cm} \chi^{2}_{LR} & = 2(LL_{constrained} – LL_{regression})\\ & = 2(-49.01 – (-54.402)) = 10.784 \end{align*} \] The p-value for the LR test with the \(\chi^{2}_{LR}\) statistic as shown above and 2 degrees of freedom (5 parameters – 3 parameters) is 0.0045. There is evidence of a lack of fit of the regression model in Eq.B. This is in line with our observations in Fig.66.
Potential remedies include considering an alternate distribution (eg: log-normal) or an alternate Box-Cox transformation of the stress variable7. Fig.4 and Table 2 show some evidence to suggest that the slope of 0.87 Mpsi line is different from the other lines. So, one could also consider fitting a model where the \(\sigma\) parameter is allowed to vary across the different levels of stress. Such behavior, where the shape parameter of the Weibull distribution increases with stress has been observed in rolling contact fatigue testing8. Some of these remedies will be discussed in a separate article. We will continue with the existing regression model in this article, but keeping in mind that the results may be biased due to lack of fit.
The ML estimates of the regression parameters can be used to estimate quantiles of the distribution at different stress levels. Table 5 below shows the 10% and 50% quantiles of the time-to-failure distribution at a stress level of 1.15 MPsi, along with the Wald 95% confidence intervals.
| ML estimate | Standard Error | Wald Lower 95% CI | Wald Upper 95% CI | |
|---|---|---|---|---|
| \(\hat{t_{0.1}}\) | 0.046 | 0.015 | 0.024 | 0.088 |
| \(\hat{t_{0.5}}\) | 0.231 | 0.049 | 0.152 | 0.349 |
Fig.7 shows a plot of the standardized residuals from the regression model vs fitted values. It is evident from this plot that the spread of the points is not the same for all 4 levels of stress. There is more variability in the larger fitted values9 as compared to the smaller fitted values. This is additional evidence that a model where the Weibull shape parameter depends on the level of stress is worth considering. The single outlier at the fitted value corresponding to 1.09 Mpsi is again observed at the bottom of the plot in Fig.7.
Figure 7: Standardized Residuals vs Fitted Values
Fig. 8 shows a Weibull plot of the standardized residuals along with the 95% confidence bands. The outlier observation corresponds to the same data point which was seen as an outlier in Fig.4 and Fig.7 and warrants a deeper investigation of this test. This outlier point is also one of the causes of the deviation from linearity of the points in Fig.8, which is again an indication of a lack of fit of the Weibull regression model. It would be interesting to compare this plot with a similar plot from a non-constant \(\sigma\) model (to be discussed in a separate article).
Figure 8: Weibull Probability Plot of Standardized Residuals
Conclusion
A time-to-failure dataset from a life test of ceramic ball bearings was analyzed using a Weibull regression model. The model assumed a constant shape parameter across all levels of the explanatory variable, stress. The regression model exhibited a lack of fit, leading to possibly biased estimates. An alternate model with different transformations of the the covariate stress or a more complex model which allows the shape parameter to vary would be worth considering. These techniques will be explored in another article.
Acknowledgements
Most of what I have learnt about time-to-event analysis is from the book Survival Analysis: Techniques for Censored and Truncated Data, Second Edition (John P. Klein and Melvin L. Moescheberger) and Statistical Methods for Reliability Data, Second Edition (William Q. Meeker, Luis A. Escobar, Francis G. Pascual).
All analyses were performed using R Statistical Software(v4.4.1; R Core Team 2024). The survival R package(v3.7.0; Therneau T 2024) was extensively used. Please refer to next section for all the packages used, their versions and the names of the package developers who deserve credit for building these amazing open source packages.
Credits for R packages used
## - Auguie B (2017). _gridExtra: Miscellaneous Functions for "Grid" Graphics_. R package version 2.3, <https://CRAN.R-project.org/package=gridExtra>.
## - Grolemund G, Wickham H (2011). "Dates and Times Made Easy with lubridate." _Journal of Statistical Software_, *40*(3), 1-25. <https://www.jstatsoft.org/v40/i03/>.
## - Jackson C (2016). "flexsurv: A Platform for Parametric Survival Modeling in R." _Journal of Statistical Software_, *70*(8), 1-33. doi:10.18637/jss.v070.i08 <https://doi.org/10.18637/jss.v070.i08>.
## - Kassambara A (2023). _ggpubr: 'ggplot2' Based Publication Ready Plots_. R package version 0.6.0, <https://CRAN.R-project.org/package=ggpubr>.
## - Kassambara A, Kosinski M, Biecek P (2024). _survminer: Drawing Survival Curves using 'ggplot2'_. R package version 0.5.0, <https://CRAN.R-project.org/package=survminer>.
## - Müller K, Wickham H (2023). _tibble: Simple Data Frames_. R package version 3.2.1, <https://CRAN.R-project.org/package=tibble>.
## - R Core Team (2024). _R: A Language and Environment for Statistical Computing_. R Foundation for Statistical Computing, Vienna, Austria. <https://www.R-project.org/>.
## - Strobl R (2022). _km.ci: Confidence Intervals for the Kaplan-Meier Estimator_. R package version 0.5-6, <https://CRAN.R-project.org/package=km.ci>.
## - Therneau T (2024). _A Package for Survival Analysis in R_. R package version 3.7-0, <https://CRAN.R-project.org/package=survival>. Terry M. Therneau, Patricia M. Grambsch (2000). _Modeling Survival Data: Extending the Cox Model_. Springer, New York. ISBN 0-387-98784-3.
## - Wickham H (2016). _ggplot2: Elegant Graphics for Data Analysis_. Springer-Verlag New York. ISBN 978-3-319-24277-4, <https://ggplot2.tidyverse.org>.
## - Wickham H (2023). _forcats: Tools for Working with Categorical Variables (Factors)_. R package version 1.0.0, <https://CRAN.R-project.org/package=forcats>.
## - Wickham H (2023). _stringr: Simple, Consistent Wrappers for Common String Operations_. R package version 1.5.1, <https://CRAN.R-project.org/package=stringr>.
## - Wickham H, Averick M, Bryan J, Chang W, McGowan LD, François R, Grolemund G, Hayes A, Henry L, Hester J, Kuhn M, Pedersen TL, Miller E, Bache SM, Müller K, Ooms J, Robinson D, Seidel DP, Spinu V, Takahashi K, Vaughan D, Wilke C, Woo K, Yutani H (2019). "Welcome to the tidyverse." _Journal of Open Source Software_, *4*(43), 1686. doi:10.21105/joss.01686 <https://doi.org/10.21105/joss.01686>.
## - Wickham H, François R, Henry L, Müller K, Vaughan D (2023). _dplyr: A Grammar of Data Manipulation_. R package version 1.1.4, <https://CRAN.R-project.org/package=dplyr>.
## - Wickham H, Henry L (2023). _purrr: Functional Programming Tools_. R package version 1.0.2, <https://CRAN.R-project.org/package=purrr>.
## - Wickham H, Hester J, Bryan J (2024). _readr: Read Rectangular Text Data_. R package version 2.1.5, <https://CRAN.R-project.org/package=readr>.
## - Wickham H, Vaughan D, Girlich M (2024). _tidyr: Tidy Messy Data_. R package version 1.3.1, <https://CRAN.R-project.org/package=tidyr>.
## - Zhu H (2024). _kableExtra: Construct Complex Table with 'kable' and Pipe Syntax_. R package version 1.4.0, <https://CRAN.R-project.org/package=kableExtra>.End
I hope you found this article informative! If you have any comments or suggestions or if you find any errors and are keen to help correct the error, please write to me at shishir909@gmail.com.
Survival Analysis: Techniques for Censored and Truncated Data, Second Edition (John P. Klein and Melvin L. Moescheberger)↩︎
McCool, J. I. (1980). Confidence limits for Weibull regression with censored data. IEEE Transactions on Reliability 29, 145–150.↩︎
Statistical Methods for Reliability Data, Second Edition (William Q. Meeker, Luis A. Escobar, Francis G. Pascual)↩︎
The points are plotted at the mid-point of the jump where the CDF increases on a Kaplan Meir curve. This plotting position is useful when assessing an ML fit (lines on the plot) graphically and to compare how well they fit the non-parametric estimates (points on the plot).↩︎
Mentioned in Chapter 12 of the aforementioned book by John P. Klein and Melvin L. Moescheberger↩︎
The paper by McCool(1980) also came to the same conclusion↩︎
The log transformation of the stress variable considered here corresponds to a Box-Cox transormation parameter \(\lambda\) = 0. Alternate transformation involves other values of \(\lambda\) that maximizes the likelihood.↩︎
Mentioned in the paper by McCool(1980)↩︎
Larger fitted values correspond to lower stress levels↩︎