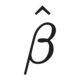This article is part of an extended series of tutorials for time-to-event (or survival) analysis. The next article is here.
Introduction
This is the second part of the article on parametric modeling1. In the previous part, we fit a Weibull regression model to a time-to-failure dataset from a life test on ceramic bearings. In this article, we will see if we can improve on the previous model by fitting a different model that can account for a varying shape parameter across different levels of the independent variable.
Similar to the first part, I have not included any R code within the article, but they are available on my Github page and can be accessed here.
Weibull Regression
The log location scale distribution model used in the first part of the article is shown in Eq. A below.
\[ \hspace{-4cm} \begin{align*} F(t;\beta_{0},\beta_{1},\sigma) & = Pr(T\le t)\\ & = \Phi\left[\frac{log(t)-(\beta_{0}+\beta_{1}log(stress))}{\sigma}\right] \tag{Eq. A} \end{align*} \] In this model, \(\sigma\) remains constant across all levels of the explanatory variable, stress. \(\Phi\) is the CDF of the standard smallest extreme value distribution. The paper by McCool(1980)2 mentions that \(\sigma\) varying with stress has been frequently observed in rolling contact fatigue testing. The plot of standardized residuals vs fitted values3 also shows that the spread of the residuals is not the same across all four levels of stress. This suggests that a model with varying \(\sigma\)4, as shown in Eq. B below, is worth considering.
\[ \hspace{-4cm} \begin{align*} F(t;\beta_{0},\beta_{1},\beta^{*}_{0},\beta^{*}_{1}) & = Pr(T\le t)\\ & = \Phi\left[\frac{log(t)-(\beta_{0}+\beta_{1}log(stress))}{exp(\beta^{*}_{0} + \beta^{*}_{1}log(stress)}\right] \tag{Eq. B} \end{align*} \] where,
\[ log(\sigma_{i}) = \beta^{*}_{0} + \beta^{*}_{1}log(stress) \] Table 1 shows the ML estimates, standard errors and the Wald 95% confidence intervals of \(\beta_{0}\), \(\beta_{1}\), \(\beta^{*}_{0}\) and \(\beta^{*}_{1}\) from the model in Eq.B.
| ML estimate | Standard Error | Wald Lower 95% CI | Wald Upper 95% CI | |
|---|---|---|---|---|
| \(\hat{\beta_{0}}\) | 0.781 | 0.160 | 0.467 | 1.094 |
| \(\hat{\beta_{1}}\) | -13.625 | 1.272 | -16.118 | -11.132 |
| \(\hat{\beta^{*}_{0}}\) | -0.139 | 0.126 | -0.386 | 0.108 |
| \(\hat{\beta^{*}_{1}}\) | -1.881 | 1.162 | -4.159 | 0.397 |
The survival package in R does not support fitting parametric models where the shape parameter depends on the covariates, like Eq. B above. I coded the Iteratively Reweighted Least Squares5 algorithm to estimate the ML estimates and their standard errors, without using any packages6. Alternatively (with some care), one could also write the log-likelihood equation and maximise it using optim() or maxLik() packages or use a package like flexsurv to directly fit parametric survival models that allow for a varying shape parameter. My limited experience in using these packages have resulted in some cases where the algorithm converged successfully while it didn’t in other cases. The standard errors reported by these packages also depend on the scale of the ML estimates and can be misleading if the estimates are very different in scale7.
The log likelihood of the regression model is -53.08 with 4 parameters. A likelihood ratio (LR) test comparing regression model above with the regression model from the previous part is shown below.
\[ \begin{align*} \hspace{-2cm} \chi^{2}_{LR} & = 2(LL_{VarShapeRegr} – LL_{ConstShapeRegr})\\ & = 2(-53.08 – (-54.402)) = 2.644 \end{align*} \] The p-value for the LR test with the \(\chi^{2}_{LR}\) statistic as shown above and 1 degree of freedom (4 parameters – 3 parameters) is 0.104. There is insufficient evidence that the varying shape parameter model is any better than the constant shape parameter model, at the 5% significance level.
Fig.1 below shows the Weibull probability plot of the varying shape parameter model. Notice that the ML lines here are not parallel, like they were in the constant shape parameter model8. Still, it doesn’t look like the fit of the lines to the non-parametric CDF estimates are very different to the fit from the constant shape parameter model.
Figure 1: Weibull plot of the varying shape regression model
Our attempt at trying to fit a slightly more complicated model did not result in a fit that is any significantly better than the constant shape model.
McCool(1981) mentions in his paper that he conjectures that a greater number of tests would affirm a stress effect on the shape parameter. Also, as previously mentioned, non-constant shape parameter has been frequently observed in rolling contact fatigue testing. Based on this additional information, which is external to the data from the life test, one could argue that the non-constant shape parameter is feasible, especially if one were to extrapolate the results to stresses outside the available range.
The 10% and 50% quantiles 9 from the varying shape parameter model and the constant shape parameter model are shown in Table 2.
| Model | Quantile | ML estimate | Standard Error | Wald Lower 95% CI | Wald Upper 95% CI |
|---|---|---|---|---|---|
| Constant Shape | \(\hat{t_{0.1}}\) | 0.046 | 0.015 | 0.024 | 0.088 |
| \(\hat{t_{0.5}}\) | 0.231 | 0.049 | 0.152 | 0.349 | |
| Varying Shape | \(\hat{t_{0.1}}\) | 0.072 | 0.026 | 0.035 | 0.147 |
| \(\hat{t_{0.5}}\) | 0.254 | 0.045 | 0.180 | 0.359 |
Fig.2 shows a plot of the standardized residuals against fitted values. Compare this plot to the corresponding plot for the constant shape parameter model 10. Notice that the spread of the points is much more equal in this plot here as compared to a model with a constant shape parameter.
Figure 2: Standardized Residuals vs Fitted Values
Fig. 3 shows a Weibull plot of the standardized residuals along with the 95% confidence bands. Comparing this plot to the corresponding plot in the previous article11 reveals that this plot suffers from a similar deviation from linearity as did the one with the constant shape parameter model.
Figure 3: Weibull Probability Plot of Standardized Residuals
Conclusion
A Weibull regression model with a varying shape parameter was fit to data from a ceramic bearings life test. A likelihood ratio test comparing this model to the constant shape parameter model gave a non-significant result, which means that there is no evidence of any improvement gained with the non-constant shape parameter model, at the 5% significance level. Nevertheless, considering that a stress effect on the shape parameter has been frequently observed in rolling contact fatigue testing, this model still has some value, especially if we need to extrapolate outside the range of stress values available outside the life test. The residual probability plot shows deviation from linearity, which is an indication that the Weibull distribution assumption is also suspect. Additional investigation could include trying a Box-Cox transformation of the independent variable or trying a different distribution (eg: log-normal).
Acknowledgements
Most of what I have learnt about time-to-event analysis is from the book Survival Analysis: Techniques for Censored and Truncated Data, Second Edition (John P. Klein and Melvin L. Moescheberger) and Statistical Methods for Reliability Data, Second Edition (William Q. Meeker, Luis A. Escobar, Francis G. Pascual).
All analyses were performed using R Statistical Software(v4.4.1; R Core Team 2024). The survival R package(v3.7.0; Therneau T 2024) was extensively used. Please refer to next section for all the packages used, their versions and the names of the package developers.
Credits for R packages used
## - Auguie B (2017). _gridExtra: Miscellaneous Functions for "Grid" Graphics_. R package version 2.3, <https://CRAN.R-project.org/package=gridExtra>.
## - Grolemund G, Wickham H (2011). "Dates and Times Made Easy with lubridate." _Journal of Statistical Software_, *40*(3), 1-25. <https://www.jstatsoft.org/v40/i03/>.
## - Jackson C (2016). "flexsurv: A Platform for Parametric Survival Modeling in R." _Journal of Statistical Software_, *70*(8), 1-33. doi:10.18637/jss.v070.i08 <https://doi.org/10.18637/jss.v070.i08>.
## - Kassambara A (2023). _ggpubr: 'ggplot2' Based Publication Ready Plots_. R package version 0.6.0, <https://CRAN.R-project.org/package=ggpubr>.
## - Kassambara A, Kosinski M, Biecek P (2024). _survminer: Drawing Survival Curves using 'ggplot2'_. R package version 0.5.0, <https://CRAN.R-project.org/package=survminer>.
## - Müller K, Wickham H (2023). _tibble: Simple Data Frames_. R package version 3.2.1, <https://CRAN.R-project.org/package=tibble>.
## - R Core Team (2024). _R: A Language and Environment for Statistical Computing_. R Foundation for Statistical Computing, Vienna, Austria. <https://www.R-project.org/>.
## - Strobl R (2022). _km.ci: Confidence Intervals for the Kaplan-Meier Estimator_. R package version 0.5-6, <https://CRAN.R-project.org/package=km.ci>.
## - Therneau T (2024). _A Package for Survival Analysis in R_. R package version 3.7-0, <https://CRAN.R-project.org/package=survival>. Terry M. Therneau, Patricia M. Grambsch (2000). _Modeling Survival Data: Extending the Cox Model_. Springer, New York. ISBN 0-387-98784-3.
## - Wickham H (2016). _ggplot2: Elegant Graphics for Data Analysis_. Springer-Verlag New York. ISBN 978-3-319-24277-4, <https://ggplot2.tidyverse.org>.
## - Wickham H (2023). _forcats: Tools for Working with Categorical Variables (Factors)_. R package version 1.0.0, <https://CRAN.R-project.org/package=forcats>.
## - Wickham H (2023). _stringr: Simple, Consistent Wrappers for Common String Operations_. R package version 1.5.1, <https://CRAN.R-project.org/package=stringr>.
## - Wickham H, Averick M, Bryan J, Chang W, McGowan LD, François R, Grolemund G, Hayes A, Henry L, Hester J, Kuhn M, Pedersen TL, Miller E, Bache SM, Müller K, Ooms J, Robinson D, Seidel DP, Spinu V, Takahashi K, Vaughan D, Wilke C, Woo K, Yutani H (2019). "Welcome to the tidyverse." _Journal of Open Source Software_, *4*(43), 1686. doi:10.21105/joss.01686 <https://doi.org/10.21105/joss.01686>.
## - Wickham H, François R, Henry L, Müller K, Vaughan D (2023). _dplyr: A Grammar of Data Manipulation_. R package version 1.1.4, <https://CRAN.R-project.org/package=dplyr>.
## - Wickham H, Henry L (2023). _purrr: Functional Programming Tools_. R package version 1.0.2, <https://CRAN.R-project.org/package=purrr>.
## - Wickham H, Hester J, Bryan J (2024). _readr: Read Rectangular Text Data_. R package version 2.1.5, <https://CRAN.R-project.org/package=readr>.
## - Wickham H, Vaughan D, Girlich M (2024). _tidyr: Tidy Messy Data_. R package version 1.3.1, <https://CRAN.R-project.org/package=tidyr>.
## - Zhu H (2024). _kableExtra: Construct Complex Table with 'kable' and Pipe Syntax_. R package version 1.4.0, <https://CRAN.R-project.org/package=kableExtra>.End
I hope you found this article informative! If you have any comments or suggestions or if you find any errors and are keen to help correct the error, please write to me at shishir909@gmail.com.
McCool, J. I. (1980). Confidence limits for Weibull regression with censored data. IEEE Transactions on Reliability 29, 145–150.↩︎
Figure 7 in the previous article.↩︎
Shape parameter = \(1/\sigma\).↩︎
P.J. Green. Iteratively reweighted least squares for maximum likelihood estimation, and some robust and resistant alternatives (with discussion). J. Royal Stat. Soc. B, 46:149 192, 1984.↩︎
I hope to write a separate blog article about this some other time.↩︎
Fig. 6 in the previous article.↩︎
Delta method was used to compute the standard errors of the quantiles.↩︎
Fig.7 in the previous article↩︎
Fig.8 in the previous article↩︎