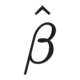This article originally appeared at Accendo Reliabilty as Competing Risks in Failure Time Data.
This article is part of an extended series of tutorials for time-to-event (or survival) analysis. The next article is here.
Introduction
In my previous blog post, I briefly discussed the survival function and the Kaplan Meir method of estimating this function from a given dataset. We applied this method to a vehicle shock absorber dataset to answer questions like “What is the probability that a vehicle shock absorber will last at least 19,000 km?”. The two different modes of failure of a shock absorber (Mode 1 and Mode 2) were ignored and were treated as the same type of failure. In the following post, we will consider the two modes of failures as two competing risks and answer questions like:
“What is the probability that a vehicle shock absorber will experience a Mode 1 failure by 19,000 km and that this failure occurs before it experiences a Mode 2 failure?”
What about the other way around? i.e.
“What is the probability that a vehicle shock absorber will experience a Mode 2 failure by 19,000 km and that this failure occurs before it experiences a Mode 1 failure?”
The following post is divided into two parts. Part I explains some of the methodologies used in the calculation of the probabilities. Part II shows the application of the survival package in R to a competing risks example, which in this case is the vehicle shock absorber data. We will start with Part II and then move on to Part I.
Part II: Application in R
First, load the data.
ShockAbsorber <- read_csv("Data/ShockAbsorber.csv")
knitr::kable((ShockAbsorber), caption = "Table 1. Shock Absorber Data", align = rep('c', 3))| Kilometers | Failure Mode | Censoring Indicator |
|---|---|---|
| 6700 | Mode1 | Failed |
| 6950 | Censored | Censored |
| 7820 | Censored | Censored |
| 8790 | Censored | Censored |
| 9120 | Mode2 | Failed |
| 9660 | Censored | Censored |
| 9820 | Censored | Censored |
| 11310 | Censored | Censored |
| 11690 | Censored | Censored |
| 11850 | Censored | Censored |
| 11880 | Censored | Censored |
| 12140 | Censored | Censored |
| 12200 | Mode1 | Failed |
| 12870 | Censored | Censored |
| 13150 | Mode2 | Failed |
| 13330 | Censored | Censored |
| 13470 | Censored | Censored |
| 14040 | Censored | Censored |
| 14300 | Mode1 | Failed |
| 17520 | Mode1 | Failed |
| 17540 | Censored | Censored |
| 17890 | Censored | Censored |
| 18450 | Censored | Censored |
| 18960 | Censored | Censored |
| 18980 | Censored | Censored |
| 19410 | Censored | Censored |
| 20100 | Mode2 | Failed |
| 20100 | Censored | Censored |
| 20150 | Censored | Censored |
| 20320 | Censored | Censored |
| 20900 | Mode2 | Failed |
| 22700 | Mode1 | Failed |
| 23490 | Censored | Censored |
| 26510 | Mode1 | Failed |
| 27410 | Censored | Censored |
| 27490 | Mode1 | Failed |
| 27890 | Censored | Censored |
| 28100 | Censored | Censored |
There are 3 different levels in the Failure Mode column above: Censored, Mode1 and Mode2. We need to convert this column to a factor vector and make sure that the first level of this factor is for censored observations1. We can do this by specifying the “levels” argument in the factor function and making sure “Censored” is the first element of the vector.
ShockAbsorber$`Failure Mode` <- factor(ShockAbsorber$`Failure Mode`,
levels = c("Censored", "Mode1", "Mode2"))
levels(ShockAbsorber$`Failure Mode`) #Verify whether censored is the first level of the factor.## [1] "Censored" "Mode1" "Mode2"In the competing risks model, every subject experiences only 1 event or is censored. They do not experience multiple events. This means that the status of any given vehicle shock absorber in our dataset can only change from “entry to Mode 1” or “entry to Mode 2” or “entry to censored”. The final state is specified by the Failure Mode column in the table. Thie initial state, i.e. entry also needs to be specified for each shock absorber and this will be done by adding a column called istate2 to the above table.
ShockAbsorber <- ShockAbsorber %>%
dplyr::mutate(istate = rep("entry", nrow(ShockAbsorber)))Next, we fit the model and display the summary.
fit_1 <- survival::survfit(
survival::Surv(time = Kilometers, event = `Failure Mode`) ~ 1,
data = ShockAbsorber,
istate = istate,
conf.type = "log",
conf.int = 0.9
)
summary(fit_1)## Call: survfit(formula = survival::Surv(time = Kilometers, event = `Failure Mode`) ~
## 1, data = ShockAbsorber, istate = istate, conf.type = "log",
## conf.int = 0.9)
##
## time n.risk n.event Pr(entry) Pr(Mode1) Pr(Mode2)
## 6700 38 1 0.974 0.0263 0.0000
## 9120 34 1 0.945 0.0263 0.0286
## 12200 26 1 0.909 0.0627 0.0286
## 13150 24 1 0.871 0.0627 0.0665
## 14300 20 1 0.827 0.1062 0.0665
## 17520 19 1 0.784 0.1497 0.0665
## 20100 12 1 0.718 0.1497 0.1318
## 20900 8 1 0.629 0.1497 0.2216
## 22700 7 1 0.539 0.2396 0.2216
## 26510 5 1 0.431 0.3473 0.2216
## 27490 3 1 0.287 0.4910 0.2216The output of the summary function above contains 3 columns: Pr(entry), Pr(Mode1) and Pr(Mode2).
Pr(entry) is the probability of a vehicle shock absorber staying in the entry state at least till a given distance. Staying in the entry state means that it has not experienced any type of failure. This is nothing but the Kaplan Meir survival probability curve! The values in this column are identical to the survival probability values we estimated in the previous blog post.
Pr(Mode1) is the probability of a vehicle shock absorber experiencing a Mode 1 failure by a given distance, while the risk of Mode 2 failure is still active (i.e. Mode 2 failure has not yet materialized, but the risk exists). Pr(Mode2) has a similar interpretation.
Pr(Mode1) and Pr(Mode2), as described above, are called cumulative incidence functions. We will touch on this topic in Part I later in this article.
Notice that for any given distance: Pr(entry) + Pr(Mode1) + Pr(Mode2) = 1.
Plotting all three probabilities on the same figure, we get
plot(
fit_1,
col = c("black", "red", "green"),
lwd = 2,
ylab = "Probability in state",
xlab = "Kilometers"
)
text(
2500,
y = c(0.7, 0.6, 0.5),
pos = 4,
labels = c(
"Black = Pr(Entry)",
"Red = Pr(Mode 1)",
"Green = Pr(Mode 2)"
)
)The plot shows that for the range of distances in our dataset, the Pr(Mode1) is higher than Pr(Mode2) at most locations, barring a few exceptions. We have data from 11 failures only, and the rest are censored values. Additional failure data would most probably help in reducing the uncertainty in our estimates and make a better comparison between the two modes. Nevertheless, we can still extract some insights. For example, at 19,000 km, the probabilities and their 90% confidence intervals (log transformed) are given below.
x = summary(fit_1, times = c(19000))
summary_19k <- data.frame(
"CI" = c(x$pstate[2], x$pstate[3]),
"90% Lower CI" = c(x$lower[2], x$lower[3]),
"90% Upper CI" = c(x$upper[2], x$upper[3]),
check.names = FALSE
)
rownames(summary_19k) <- c("Pr(Mode 1)", "Pr(Mode 2)")
summary_19k <- round(summary_19k, digits = 2)
knitr::kable((summary_19k), caption = "Table 2. Summary Table", align = rep('c', 3))## Warning in attr(x, "align"): 'xfun::attr()' is deprecated.
## Use 'xfun::attr2()' instead.
## See help("Deprecated")## Warning in attr(x, "format"): 'xfun::attr()' is deprecated.
## Use 'xfun::attr2()' instead.
## See help("Deprecated")| CI | 90% Lower CI | 90% Upper CI | |
|---|---|---|---|
| Pr(Mode 1) | 0.15 | 0.07 | 0.33 |
| Pr(Mode 2) | 0.07 | 0.02 | 0.21 |
The probability of a Mode 1 failure within 19,000 km, while the risk of a Mode 2 failure is active is 0.15 with a 90% confidence interval (0.03,0.27). We can make a similar statement about Mode 2 failure by 19,000 km using the quantities in the table above.
Part I: Methodology
Suppose we have \(l = 1,..,m\) competing risks. We are interested in finding out the probability of a particular risk \(l\) failure (event) occurring before time \(t\), while all the other \(m-1\) risks are acting on the subject3. This is also called crude probability and is expressed by the cumulative incidence funcion.
\[F_{l}(t) = P[T\le t,\delta = l]\] where \(T\) is the time-to-event random variable and \(\delta\) is an indicator for risk \(l\).
For non-parametric methods, the cumulative incidence function for risk \(l\) is given by
\[CI_{l}(t) = 0 \quad \text{ if }t<t_{1}\\\] and \[CI_{l}(t) = \sum_{t_{i} \le t} \Bigg\{\prod_{j=1}^{i-1} [1 – \frac{(d_{j} + r_{j})}{Y_{j}}]\Bigg\}\frac{r_{i}}{Y_{i}} \quad \text{ if }t\ge t_{1}\\\] where \(t_{i} = \{t_{1},t_{2}..\}\) are the event times in our dataset (not censored). \(r_{j}\) is the number of events of risk \(l\) at time \(t_{j}\) and \(d_{j}\) is the number of events of all the other competing risks at time \(t_{j}\).
Notice that the term inside the braces is the Kaplan Meir estimate of the survival function evaluated just before \(t_{i}\) i.e.
\[CI_{l}(t) = \sum_{t_{i} \le t} \Bigg\{\hat{S}(t_{i-})\Bigg\}\frac{r_{i}}{Y_{i}} \quad \text{ if }t\ge t_{1}\\\]
In the vehicle shock absorber example, we have 2 competing risks, Mode 1 and Mode 2. So, \(l = 1,2\). The following table gives the values of the quantities required to calculate the cumulative incidence function as well as the cumulative incidence function at the different event times (distances).
knitr::kable((calculation_table),
caption = "Table 3. Calculation Table",
align = rep('c', 4))## Warning in attr(x, "align"): 'xfun::attr()' is deprecated.
## Use 'xfun::attr2()' instead.
## See help("Deprecated")## Warning in attr(x, "format"): 'xfun::attr()' is deprecated.
## Use 'xfun::attr2()' instead.
## See help("Deprecated")| \(t_{i}\) | \(r_{i}\) | \(d_{i}\) | \(Y_{i}\) | \({S}(t_{i-})\) | \(Pr(Mode 1)\) |
|---|---|---|---|---|---|
| 6700 | 1 | 0 | 38 | 1.0000 | 0.0263 |
| 9120 | 0 | 1 | 34 | 0.9737 | 0.0263 |
| 12200 | 1 | 0 | 26 | 0.9450 | 0.0627 |
| 13150 | 0 | 1 | 24 | 0.9087 | 0.0627 |
| 14300 | 1 | 0 | 20 | 0.8708 | 0.1062 |
| 17520 | 1 | 0 | 19 | 0.8273 | 0.1497 |
| 20100 | 0 | 1 | 12 | 0.7838 | 0.1497 |
| 20900 | 0 | 1 | 8 | 0.7184 | 0.1497 |
| 22700 | 1 | 0 | 7 | 0.6286 | 0.2396 |
| 26510 | 1 | 0 | 5 | 0.5388 | 0.3473 |
| 27490 | 1 | 0 | 3 | 0.4311 | 0.4910 |
The values of the cumulative incidence function in the above table, obtained using the aforementioned formula match the values we get from the survival package.
The fifth column in the above table is the estimated survival function4 just before time \(t_{i}\).
The variance of the cumulative incidence function for a particular risk \(l\) is estimated by
\[\hat{V}[\hat{CI_{l}}(t)] = \sum_{t_{i} \le t} \hat{S}(t_{i})^2\Bigg\{[\hat{CI_{l}}(t) – \hat{CI_{l}}(t_{i})]^2\frac{r_{i}+d_{i}}{Y_{i}^2}+[1-2(\hat{CI_{l}(t)}-\hat{CI_{l}}(t_{i}))]\frac{r_{i}}{Y_{i}^2}\Bigg\}\] Plugging the appropriate values in the above formula and taking the square root will yield the same standard error values from the model fit using the survival package. The standard errors can then be used to calculate confidence intervals.
Acknowledgements
Most of what I have learnt about time-to-event analysis is from the book Survival Analysis: Techniques for Censored and Truncated Data, Second Edition (John P. Klein and Melvin L. Moescheberger).
The dataset I have used above is used in one of the examples in the book Statistical Methods for Reliability Data, Second Edition (William Q. Meeker, Luis A. Escobar, Francis G. Pascual).
This article’s format is a style that Edward Tufte uses in his books and handouts. I have used the tufte library in R and am grateful to the authors of this package. I should also mention that I found out about this style when I stumbled across an article on Survival Analysis by Mark Bounthavong, which was also written using the tufte package.
End
I hope you enjoyed reading this blog post! If you have any comments or suggestions or if you find any errors and are keen to help correct the error, please write to me at shishir909@gmail.com.
This is a requirement specified in the survival package documentation.↩︎
istate stands for initial state↩︎
In other words, it is the probability of a particular risk \(l\) failure occurring before time \(t\), and that it occurs before any of the other competing risks occur.↩︎
Note that this should be \(\hat{S}(t_{i-})\) and not \({S}(t_{i-})\) since it is an estimate. I was unable to include the “hat” on top of the \(S\) in the table using the knitr package.↩︎