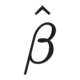This article is part of an extended series of tutorials for time-to-event (or survival) analysis. The next article is here.
Introduction
This article is a continuation of the series of articles where I apply the concepts learnt from the book Survival Analysis: Techniques for Censored and Truncated Data, Second Edition (John P. Klein and Melvin L. Moescheberger) to datasets from reliability. The book focuses on applications in biology and medicine, but the methods described are equally applicable to other fields like reliability and quality assurance.
The last article1 shows an application of a non-parametric log rank test where the aim was to test whether failure rates are different among two or more groups. This article is a continuation of the non-parametric testing methods by extending its application to a test that has power to detect a trend in the failure rate. The second application demonstrated here extends the log rank test by including an adjustment for confounding variables that could possibly affect the failure rates. This is done using a stratified test.
Test for trend
To illustrate a test for trend, we will use the PartA dataset, which contains data from an experiment conducted to compare three life test operators. The operators perform life testing on a machine tool part and the manufacturer suspects that the manual nature of the life test contributes to variability in the results of the life tests. This dataset is from another excellent book2 on the topic of statistical analysis of reliability data and is available on the book’s student companion website. It can also be accessed from DataShare, Iowa State University’s open data repository through this link.
Load the dataset
PartA <- read_csv("Data/PartA.csv") ## Rows: 60 Columns: 2
## ── Column specification ────────────────────────────────────────────────────────
## Delimiter: ","
## chr (1): Operator Number
## dbl (1): Thousands of Cycles
##
## ℹ Use `spec()` to retrieve the full column specification for this data.
## ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.PartA <- PartA %>%
dplyr::mutate(Status = rep(1,nrow(PartA))) %>%
dplyr::rename(Cycles = `Thousands of Cycles`,
Operator = `Operator Number`)
knitr::kable((PartA), caption = "Table 1. Part A Life Test", align = rep('c', 3), table.envir = 'table*') %>%
kableExtra::kable_styling("striped", full_width = T, position = "left") %>%
kableExtra::scroll_box(height = "200px")## Warning in attr(x, "align"): 'xfun::attr()' is deprecated.
## Use 'xfun::attr2()' instead.
## See help("Deprecated")
## Warning in attr(x, "align"): 'xfun::attr()' is deprecated.
## Use 'xfun::attr2()' instead.
## See help("Deprecated")| Cycles | Operator | Status |
|---|---|---|
| 23 | Op1 | 1 |
| 54 | Op1 | 1 |
| 47 | Op1 | 1 |
| 50 | Op1 | 1 |
| 28 | Op1 | 1 |
| 22 | Op1 | 1 |
| 28 | Op1 | 1 |
| 6 | Op1 | 1 |
| 41 | Op1 | 1 |
| 39 | Op1 | 1 |
| 17 | Op1 | 1 |
| 21 | Op1 | 1 |
| 21 | Op1 | 1 |
| 15 | Op1 | 1 |
| 23 | Op1 | 1 |
| 30 | Op1 | 1 |
| 57 | Op1 | 1 |
| 26 | Op1 | 1 |
| 22 | Op1 | 1 |
| 64 | Op1 | 1 |
| 30 | Op2 | 1 |
| 38 | Op2 | 1 |
| 18 | Op2 | 1 |
| 68 | Op2 | 1 |
| 107 | Op2 | 1 |
| 84 | Op2 | 1 |
| 83 | Op2 | 1 |
| 38 | Op2 | 1 |
| 64 | Op2 | 1 |
| 32 | Op2 | 1 |
| 44 | Op2 | 1 |
| 77 | Op2 | 1 |
| 41 | Op2 | 1 |
| 87 | Op2 | 1 |
| 50 | Op2 | 1 |
| 26 | Op2 | 1 |
| 147 | Op2 | 1 |
| 34 | Op2 | 1 |
| 25 | Op2 | 1 |
| 88 | Op2 | 1 |
| 214 | Op3 | 1 |
| 143 | Op3 | 1 |
| 263 | Op3 | 1 |
| 127 | Op3 | 1 |
| 40 | Op3 | 1 |
| 87 | Op3 | 1 |
| 161 | Op3 | 1 |
| 46 | Op3 | 1 |
| 73 | Op3 | 1 |
| 114 | Op3 | 1 |
| 239 | Op3 | 1 |
| 346 | Op3 | 1 |
| 133 | Op3 | 1 |
| 129 | Op3 | 1 |
| 284 | Op3 | 1 |
| 22 | Op3 | 1 |
| 240 | Op3 | 1 |
| 181 | Op3 | 1 |
| 217 | Op3 | 1 |
| 272 | Op3 | 1 |
Note that there is no censoring in this dataset, but the test for trend is applicable even in the presence of right censored observations.
The authors of the book on statistical methods for reliability data (mentioned above) use this dataset to conduct a log-rank test, which tests whether there is any statistically significant difference in the failure rates of the three operators. This was the original context of this problem.
Let us suppose that in addition to the failure rates being different, the manufacturer also suspects a trend in the failure rate comparisons i.e. the manufacturer suspects that Operator 1’s failure rate is greater than Operator 2’s rate, which in turn is greater than Operator 3’s failure rate3. We will test for this trend in the data using a test that has power to detect a trend. The null and alternate hypothesis test is set up as shown below.
\[ \begin{align*} &H_0: h_{Op_1}(t) = h_{Op_2}(t) = h_{Op_3}(t) \quad \text{for all } t \leq \tau, \quad \text{versus} \\ \\ &H_A: h_{Op_1}(t) \geq h_{Op_2}(t) \geq h_{Op_3}(t) \quad \text{for some} \, t \leq \tau \text{, with at least one strict inequality}. \quad \end{align*} \]
h(t) is the failure rate and \(\tau\) is the largest time4 at which all 3 operators have at least one observation at risk.
Kaplan Meir curves for the 3 operators are shown below.
fit_PartA <- survival::survfit(
Surv(time = Cycles, event = Status) ~ Operator,
data = PartA,
conf.type = "log",
conf.int = 0.95
)
survminer::ggsurvplot(
fit_PartA,
data = PartA,
risk.table = T,
conf.int = T
)Clearly, the survival curves for the 3 operators are very different. The overlap between the confidence intervals is also low.
First, a log rank test is performed, which tests the following hypothesis:
\[ \begin{align*} &H_0: h_{Op_1}(t) = h_{Op_2}(t) = h_{Op_3}(t) \quad \text{for all } t \leq \tau, \quad \text{versus} \\ \\ &H_A: \text{at least one of the failure rates is different for some } t \leq \tau \quad \end{align*} \]
Log rank test using the survdiff function from the survival package is shown below.
diff1 <- survival::survdiff(Surv(time = Cycles, event = Status) ~ Operator,
data = PartA,
rho = 0) #rho = 0 for a log rank test
diff1## Call:
## survival::survdiff(formula = Surv(time = Cycles, event = Status) ~
## Operator, data = PartA, rho = 0)
##
## N Observed Expected (O-E)^2/E (O-E)^2/V
## Operator=Op1 20 20 7.02 23.97 31.63
## Operator=Op2 20 20 14.70 1.91 2.88
## Operator=Op3 20 20 38.28 8.73 32.62
##
## Chisq= 46.1 on 2 degrees of freedom, p= 1e-10The p-value for the chi-squared statistic is very small, clearly showing that there is evidence of a difference in the failure rates at the 5% significance level.
Next, we investigate whether there is evidence of a trend. I was unable to find a function in the survival package that can directly conduct a non-parametric test for trend. The test statistic will have to be calculated manually. This test statistic is still based on the test statistic for a log rank test that we conducted above. Hence, we can rely on the survival package for some of the quantities required to calculate the trend test statistic.
In order to conduct a trend test, we first select a sequence of scores \(a_{1} < a_{2} < … a_{K}\). We can use any increasing set of scores. We will use a score of \(a_{1} = 3\) for Operator 1, \(a_{2} = 2\) for Operator 2 and \(a_{3} = 1\) for Operator 35.
The test statistic is given by
\[ Z = \frac{\sum_{j=1}^{K} a_{j}Z_{j}(\tau)}{\sqrt{\sum_{j=1}^{K}\sum_{q=1}^{K} a_{j}a_{q}\hat{\sigma}_{jq}}} \] where \(K\) is the number of groups, which is 3 in our case and \(Z_{j}(\tau)\) is the sum of the weighted6 differences between observed and expected events at every event time. This can be directly obtained from the output of the log rank test above. We get \(Z_{1} = Observed – Expected = 20 – 7.2 = 12.8\). Similarly, \(Z_{2} = 5.3\) and \(Z_{3} = -18.28\)
When the null hypothesis is true and the sample sizes are sufficiently large, then this test statistic has a standard normal distribution.
The variance-covariance matrix of the \(Z_{j}\)’s can be obtained from the survdiff object of the log-rank test, as shown below.
diff1[["var"]]## [,1] [,2] [,3]
## [1,] 5.322160 -2.417677 -2.904483
## [2,] -2.417677 9.755310 -7.337633
## [3,] -2.904483 -7.337633 10.242116The values of \(\hat{\sigma_{jg}}\) in the formula for the test statistic are obtained from the above variance-covariance matrix.
Plugging these values into the formula for the test statistic, we get
\[ Z = \frac{(3\times 12.8) + (2\times 5.3) + (1\times -18.28)}{\sqrt{(3\times3\times5.32) + (3\times2\times -2.41) + (3\times1\times -2.90)+ \\ (2\times3\times -2.41) + (2\times2\times 9.75) + (2\times1\times -7.33)+ \\ (1\times3\times -2.90) + (1\times2\times -7.33) + (1\times1\times 10.24)}} \] This leads to a a value of the test statistic \(Z = 6.62\). The p-value is then calculated as:
2*(1-pnorm(6.62))## [1] 3.591993e-11The low p-value suggests that there is a strong evidence that the trend in the failure rates are as per the a priori information that the manufacturer suspected.
Stratified Tests
Stratified test conducts a test of hypothesis of difference in the failure rates, after adjusting for confounding variables. This is illustrated through an example below.
The capacitor dataset from the survival package in R will be used7. This dataset consists of data from an experiment on the life of glass capacitors as a function of operating temperature and voltage. Testing at each combination of temperature and voltage was terminated after the fourth failure8. This dataset is also available in the book previously mentioned9 and can be accessed through the book’s student companion website or from DataShare, Iowa State University’s open data repository through this link.
The book authors analyzed this data using a parametric regression method. In this article, we will use it to perform a non-parametric stratified test for difference in hazard rates.
data(reliability, package = 'survival')
capacitor <- capacitor %>%
dplyr::select(!fail) #Removing the column fail
knitr::kable(capacitor, caption = "Table 1. Capacitor Data", align = rep('c', 5), table.envir = 'table*') %>%
kableExtra::kable_styling("striped", full_width = T, position = "left") %>%
kableExtra::scroll_box(height = "200px")## Warning in attr(x, "align"): 'xfun::attr()' is deprecated.
## Use 'xfun::attr2()' instead.
## See help("Deprecated")
## Warning in attr(x, "align"): 'xfun::attr()' is deprecated.
## Use 'xfun::attr2()' instead.
## See help("Deprecated")| temperature | voltage | time | status |
|---|---|---|---|
| 170 | 200 | 439 | 1 |
| 170 | 200 | 904 | 1 |
| 170 | 200 | 1092 | 1 |
| 170 | 200 | 1105 | 1 |
| 170 | 250 | 572 | 1 |
| 170 | 250 | 690 | 1 |
| 170 | 250 | 904 | 1 |
| 170 | 250 | 1090 | 1 |
| 170 | 300 | 315 | 1 |
| 170 | 300 | 315 | 1 |
| 170 | 300 | 439 | 1 |
| 170 | 300 | 628 | 1 |
| 170 | 350 | 258 | 1 |
| 170 | 350 | 258 | 1 |
| 170 | 350 | 347 | 1 |
| 170 | 350 | 588 | 1 |
| 180 | 200 | 959 | 1 |
| 180 | 200 | 1065 | 1 |
| 180 | 200 | 1065 | 1 |
| 180 | 200 | 1087 | 1 |
| 180 | 250 | 216 | 1 |
| 180 | 250 | 315 | 1 |
| 180 | 250 | 455 | 1 |
| 180 | 250 | 473 | 1 |
| 180 | 300 | 241 | 1 |
| 180 | 300 | 315 | 1 |
| 180 | 300 | 332 | 1 |
| 180 | 300 | 380 | 1 |
| 180 | 350 | 241 | 1 |
| 180 | 350 | 241 | 1 |
| 180 | 350 | 435 | 1 |
| 180 | 350 | 455 | 1 |
| 170 | 200 | 1105 | 0 |
| 170 | 200 | 1105 | 0 |
| 170 | 200 | 1105 | 0 |
| 170 | 200 | 1105 | 0 |
| 170 | 250 | 1090 | 0 |
| 170 | 250 | 1090 | 0 |
| 170 | 250 | 1090 | 0 |
| 170 | 250 | 1090 | 0 |
| 170 | 300 | 628 | 0 |
| 170 | 300 | 628 | 0 |
| 170 | 300 | 628 | 0 |
| 170 | 300 | 628 | 0 |
| 170 | 350 | 588 | 0 |
| 170 | 350 | 588 | 0 |
| 170 | 350 | 588 | 0 |
| 170 | 350 | 588 | 0 |
| 180 | 200 | 1087 | 0 |
| 180 | 200 | 1087 | 0 |
| 180 | 200 | 1087 | 0 |
| 180 | 200 | 1087 | 0 |
| 180 | 250 | 473 | 0 |
| 180 | 250 | 473 | 0 |
| 180 | 250 | 473 | 0 |
| 180 | 250 | 473 | 0 |
| 180 | 300 | 380 | 0 |
| 180 | 300 | 380 | 0 |
| 180 | 300 | 380 | 0 |
| 180 | 300 | 380 | 0 |
| 180 | 350 | 455 | 0 |
| 180 | 350 | 455 | 0 |
| 180 | 350 | 455 | 0 |
| 180 | 350 | 455 | 0 |
A “1” in the status column indicates a failure and a “0” indicates a right censored observation.
For the purpose of this exercise, let us suppose that our interest lies in comparing the failure rates of capacitors operating at a temperature of 170 C versus 180 C, but adjusting for the voltage. That is, we want to test the following hypothesis:
\[ \begin{align*} &H_0: h_{170C,V}(t) = h_{180C,V}(t) \quad \text{for V = 200, 250, 300, 350} \text{ and } t \leq \tau, \quad \text{versus} \\ \\ &H_A: h_{170C,V}(t) \, \text{is different to} \, h_{180C,V}(t) \, \text{for at least one V and for some} \, t \leq \tau. \quad \end{align*} \]
A plot of the Kaplan Meir survival curve for the two operating temperatures is shown below.
fit_capacitor <- survival::survfit(
Surv(time = time, event = status) ~ factor(temperature),
data = capacitor,
conf.type = "log",
conf.int = 0.95
)
survminer::ggsurvplot(
fit_capacitor,
data = capacitor,
risk.table = T,
conf.int = T
)Note that the above curve ignores the voltage variable and only compares the curves for the two operating temperature groups.
Next, we conduct a log rank test, again ignoring the voltage. We will get to the stratified test later, which will take voltage into consideration.
survival::survdiff(
Surv(time = time, event = status, type = 'right') ~ factor(temperature),
data = capacitor,
rho = 0
)## Call:
## survival::survdiff(formula = Surv(time = time, event = status,
## type = "right") ~ factor(temperature), data = capacitor,
## rho = 0)
##
## N Observed Expected (O-E)^2/E (O-E)^2/V
## factor(temperature)=170 32 16 19.8 0.744 2.19
## factor(temperature)=180 32 16 12.2 1.214 2.19
##
## Chisq= 2.2 on 1 degrees of freedom, p= 0.1The p-value of 0.1 suggests that there is no evidence of a difference in failure rates between capacitors operating at the 2 temperatures at the 5% significance level10.
Next, we conduct a stratified test that takes the confounding variable voltage into account11.
survival::survdiff(
Surv(time = time, event = status, type = 'right') ~ factor(temperature) + strata(factor(voltage)),
data = capacitor,
rho = 0
)## Call:
## survival::survdiff(formula = Surv(time = time, event = status,
## type = "right") ~ factor(temperature) + strata(factor(voltage)),
## data = capacitor, rho = 0)
##
## N Observed Expected (O-E)^2/E (O-E)^2/V
## factor(temperature)=170 32 16 20.8 1.12 4.25
## factor(temperature)=180 32 16 11.2 2.09 4.25
##
## Chisq= 4.2 on 1 degrees of freedom, p= 0.04The p-value of 0.04 suggests that there is evidence of difference in the failure rates of the capacitors operating at 170 C vs 180 C at the 5% significance level, once the comparison is adjusted for different voltages.
What does this mean though? It means that we have found evidence against at least one of the following comparisons, at the 5% significance level:
\[ \begin{align*} h_{170 C,200 V}(t) = h_{180 C,200 V}(t),\\ h_{170 C,250 V}(t) = h_{180 C,250 V}(t), \\ h_{170 C,300 V}(t) = h_{180 C,300 V}(t), \\ h_{170 C,350 V}(t) = h_{180 C,350 V}(t). \end{align*} \] The un-stratified log rank test did not suggest any difference in the failure rates at the two separate operating temperatures, but there was evidence once the comparison adjusted for voltage.
Comparing the 4 different stratas (voltages) separately, we get the following.
survival::survdiff(
Surv(time = time, event = status, type = 'right') ~ factor(temperature),
data = capacitor[which(capacitor$voltage==200),],
rho = 0
)## Call:
## survival::survdiff(formula = Surv(time = time, event = status,
## type = "right") ~ factor(temperature), data = capacitor[which(capacitor$voltage ==
## 200), ], rho = 0)
##
## N Observed Expected (O-E)^2/E (O-E)^2/V
## factor(temperature)=170 8 4 4.86 0.153 0.515
## factor(temperature)=180 8 4 3.14 0.238 0.515
##
## Chisq= 0.5 on 1 degrees of freedom, p= 0.5survival::survdiff(
Surv(time = time, event = status, type = 'right') ~ factor(temperature),
data = capacitor[which(capacitor$voltage==250),],
rho = 0
)## Call:
## survival::survdiff(formula = Surv(time = time, event = status,
## type = "right") ~ factor(temperature), data = capacitor[which(capacitor$voltage ==
## 250), ], rho = 0)
##
## N Observed Expected (O-E)^2/E (O-E)^2/V
## factor(temperature)=170 8 4 6.22 0.792 5.03
## factor(temperature)=180 8 4 1.78 2.769 5.03
##
## Chisq= 5 on 1 degrees of freedom, p= 0.02survival::survdiff(
Surv(time = time, event = status, type = 'right') ~ factor(temperature),
data = capacitor[which(capacitor$voltage==300),],
rho = 0
)## Call:
## survival::survdiff(formula = Surv(time = time, event = status,
## type = "right") ~ factor(temperature), data = capacitor[which(capacitor$voltage ==
## 300), ], rho = 0)
##
## N Observed Expected (O-E)^2/E (O-E)^2/V
## factor(temperature)=170 8 4 5.15 0.255 0.945
## factor(temperature)=180 8 4 2.85 0.460 0.945
##
## Chisq= 0.9 on 1 degrees of freedom, p= 0.3survival::survdiff(
Surv(time = time, event = status, type = 'right') ~ factor(temperature),
data = capacitor[which(capacitor$voltage==350),],
rho = 0
)## Call:
## survival::survdiff(formula = Surv(time = time, event = status,
## type = "right") ~ factor(temperature), data = capacitor[which(capacitor$voltage ==
## 350), ], rho = 0)
##
## N Observed Expected (O-E)^2/E (O-E)^2/V
## factor(temperature)=170 8 4 4.6 0.0776 0.214
## factor(temperature)=180 8 4 3.4 0.1049 0.214
##
## Chisq= 0.2 on 1 degrees of freedom, p= 0.6The p-value is significant at 5% only for the 250 V strata. Since the number of events in this dataset is very small, these results must be interpreted with caution12.
Conclusion
Application of two non-parametric tests were demonstrated in this article – one for testing for a trend in the failure rate and another for adjusting for confounding variables in the comparison, using a stratified test. The stratified test is feasible when the number of stratas are not very large or when a continuous confounding variable can be discretized into a workable number of stratas. The other approach in such problems is to use regression methods – parametric or semi parametric, in order to account for confounding variables.
There are a few points that we must keep in mind when applying the tests discussed so far in this article as well as the previous article (log rank, stratified and trend).
The observations are assumed to be independent i.e. the time to failure of the observations are not dependent on each other in any way.
Censoring is assumed to be non-informative i.e. event times (failure times) and censoring times are independent of each other.
The log rank tests have optimal power to detect difference in failure rates when the hazards (failure rates) between the groups are proportional i.e. the failure rate curves of the groups do not cross. When the hazard rate curves do cross, early positive differnces may be cancelled out by later negative differences (or vice versa) and may mislead us into concluding that there is no difference between the groups13.
Acknowledgements
Most of what I have learnt about time-to-event analysis is from the book Survival Analysis: Techniques for Censored and Truncated Data, Second Edition (John P. Klein and Melvin L. Moescheberger).
The datasets in this article are from the book Statistical Methods for Reliability Data, Second Edition (William Q. Meeker, Luis A. Escobar, Francis G. Pascual). This has also been an excellent resource in my journey to learn about modeling failure times.
All analyses were performed using R Statistical Software(v4.4.1; R Core Team 2024). The survival R package(v3.7.0; Therneau T 2024) was extensively used. Please refer to next section for all the packages used, their versions and the names of the package developers who deserve credit for building these amazing open source packages.
Credits for R packages used
report::cite_packages()## - Grolemund G, Wickham H (2011). "Dates and Times Made Easy with lubridate." _Journal of Statistical Software_, *40*(3), 1-25. <https://www.jstatsoft.org/v40/i03/>.
## - Kassambara A (2023). _ggpubr: 'ggplot2' Based Publication Ready Plots_. R package version 0.6.0, <https://CRAN.R-project.org/package=ggpubr>.
## - Kassambara A, Kosinski M, Biecek P (2024). _survminer: Drawing Survival Curves using 'ggplot2'_. R package version 0.5.0, <https://CRAN.R-project.org/package=survminer>.
## - Müller K, Wickham H (2023). _tibble: Simple Data Frames_. R package version 3.2.1, <https://CRAN.R-project.org/package=tibble>.
## - R Core Team (2024). _R: A Language and Environment for Statistical Computing_. R Foundation for Statistical Computing, Vienna, Austria. <https://www.R-project.org/>.
## - Therneau T (2024). _A Package for Survival Analysis in R_. R package version 3.7-0, <https://CRAN.R-project.org/package=survival>. Terry M. Therneau, Patricia M. Grambsch (2000). _Modeling Survival Data: Extending the Cox Model_. Springer, New York. ISBN 0-387-98784-3.
## - Wickham H (2016). _ggplot2: Elegant Graphics for Data Analysis_. Springer-Verlag New York. ISBN 978-3-319-24277-4, <https://ggplot2.tidyverse.org>.
## - Wickham H (2023). _forcats: Tools for Working with Categorical Variables (Factors)_. R package version 1.0.0, <https://CRAN.R-project.org/package=forcats>.
## - Wickham H (2023). _stringr: Simple, Consistent Wrappers for Common String Operations_. R package version 1.5.1, <https://CRAN.R-project.org/package=stringr>.
## - Wickham H, Averick M, Bryan J, Chang W, McGowan LD, François R, Grolemund G, Hayes A, Henry L, Hester J, Kuhn M, Pedersen TL, Miller E, Bache SM, Müller K, Ooms J, Robinson D, Seidel DP, Spinu V, Takahashi K, Vaughan D, Wilke C, Woo K, Yutani H (2019). "Welcome to the tidyverse." _Journal of Open Source Software_, *4*(43), 1686. doi:10.21105/joss.01686 <https://doi.org/10.21105/joss.01686>.
## - Wickham H, François R, Henry L, Müller K, Vaughan D (2023). _dplyr: A Grammar of Data Manipulation_. R package version 1.1.4, <https://CRAN.R-project.org/package=dplyr>.
## - Wickham H, Henry L (2023). _purrr: Functional Programming Tools_. R package version 1.0.2, <https://CRAN.R-project.org/package=purrr>.
## - Wickham H, Hester J, Bryan J (2024). _readr: Read Rectangular Text Data_. R package version 2.1.5, <https://CRAN.R-project.org/package=readr>.
## - Wickham H, Vaughan D, Girlich M (2024). _tidyr: Tidy Messy Data_. R package version 1.3.1, <https://CRAN.R-project.org/package=tidyr>.
## - Zhu H (2024). _kableExtra: Construct Complex Table with 'kable' and Pipe Syntax_. R package version 1.4.0, <https://CRAN.R-project.org/package=kableExtra>.End
I hope you enjoyed reading this blog post! If you have any comments or suggestions or if you find any errors and are keen to help correct the error, please write to me at shishir909@gmail.com.
Hypothesis Testing of Failure Time Data: Part I can be accessed here↩︎
Statistical Methods for Reliability Data, Second Edition (William Q. Meeker, Luis A. Escobar, Francis G. Pascual)↩︎
Note that a test for trend should only be applied when there is some a priori information that the alternatives are ordered.↩︎
Time is measured in cycles in this example↩︎
\(a_{1}\) gets the highest score because the a priori information from the manufacturer is that Operator 1’s failure rate is the highest, followed by Operator 2.↩︎
For the log rank test, the common weight shared by each group is 1, which means that the weights in the weighted difference is the number at risk at that particular event time. Refer to any of the above mentioned book for details on the log rank test.↩︎
The reliability datasets available in the survival package references “Meeker and Escobar, Statistical Methods for Reliability Data, 1998.”↩︎
This is called Type II censoring↩︎
Statistical Methods for Reliability Data, Second Edition (William Q. Meeker, Luis A. Escobar, Francis G. Pascual)↩︎
There is a decent amount of overlap between the confidence intervals of the two curves in the above Kaplan-Meir plot, which again is not very surprising, considering that the log rank test did not reveal any evidence of difference in hazard rates either.↩︎
This is done by using the strata function within the survdiff function, as shown below↩︎
The authors of the book treat this dataset using a parametric regression model, which is a much more detailed analysis and can be found in Chapter 17 of the book.↩︎
If the hazards are not proportional, there are other tests, like Renyi type tests, that can be conducted to test for a difference in the failure rates.↩︎